- *Corresponding Author:
- Dinorah Varges
Physiology and Pharmacology Department, Veterinary Medicine School, México
E-mail: dinorah.vestrada@gmail.com
| Date of Submission | 26 November 2018 |
| Date of Revision | 19 January 2019 |
| Date of Acceptance | 15 May 2019 |
| Indian J Pharm Sci 2019;81(4):608-617 |
This is an open access article distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License, which allows others to remix, tweak, and build upon the work non-commercially, as long as the author is credited and the new creations are licensed under the identical terms
Abstract
The aim of this study was to establish and validate an in vitro-in vivo correlation that could predict the bioavailability of 4 oral long-acting formulations of doxycycline hyclate, acrylic acid and polymethacrylate matrices prepared using various proportions of doxycycline:acrylic acid:polymethacrylate for formulation 1 (1:0.25:0.0035), formulation 2 (1:0.5:0.0075), formulation 3 (1:1:0.015) and formulation 4 (1:2:0.0225) and a sample of doxycycline without excipients. In vitro dissolution profiles were obtained in phosphate buffer and hydrochloric acid media, which were fitted to several mathematical models. Plasma concentrations were obtained from 48 healthy dogs to achieve in vivo profiles. Therapeutic concentrations were observed for 60 h for formulation 1 and 4, 48 h for formulation 2 and 3 and 24 h for the sample of doxycycline. None of the pharmacokinetic parameter differed significantly between formulation 1 and 2 or between formulation 3 and 4; however, doxycycline differed significantly in comparison. The in vivo-in vitro correlation coefficient obtained from point-to-point analysis >0.999 for formulation 3 and 4 and >0.9581 for the others. To validate the model, the absorbed fractions for all formulations were estimated to predict plasma concentration profiles. In conclusion, adequate in vitro-in vivo correlation was established for long-acting formulations of doxycycline indicating that in vitro dissolution tests could be used as a surrogate for bioavailability studies.
Keywords
Dissolution, bioavailability, in vitro models, oral drug delivery, polymeric drugs
Doxycycline (DOX) is a second-generation tetracycline used for treatment of several infections in both humans and domestic animal species. DOX has broadspectrum activity against aerobic and anaerobic[1] microorganisms, as well as antiinflammatory and antineoplastic activities through inhibition of matrix metalloproteinases produced by inflammatory cells[2,3]. DOX showed better clinical efficiency at low concentrations, 2 to 4 times that of the minimum inhibitory concentration (MIC) against microorganism being treated. DOX inhibited growth of microorganisms in a time-dependent way[4].
DOX use has sometimes been limited due to adverse reactions, such as oesophagus and stomach irritation or the risk of ulceration and vomiting following oral administration[5-7]. Controlled-release DOX formulations might reduce adverse effects and improve the DOX efficacy during lengthy treatment periods. By extending the frequency of administration intervals, less gastrointestinal tract irritation, thereby improving therapy compliance[8,9]. Drug absorption following oral administration is dependent on release from the pharmaceutical formulation, dissolution in the physiological medium, and permeability across the gastrointestinal tract. Dissolution tests are an important tool for guiding the development of new formulations, manufacturing process evaluation, and assessment of lot-to-lot quality[10,11]. In vitro methods could be more useless if the analytical conditions allow an analogy with in vivo data, and subsequently, an in vivo-in vitro correlation (IVIVC) can be established[10,11].
IVIVC deals with a (preferably linear) relationship between an in vitro characteristic and a biological parameter[10,11]. The FDA guidance document states that the main objective in developing and evaluating an IVIVC is to enable the dissolution test to serve as a surrogate for an in vivo bioavailability study. The IVIVC is used in formulation development work as well as during the scale up and post approval changes[12]. IVIVC categories are described in the FDA guidance document as, level A, level B, level C and multiple level C. Out of these 4 categories, level A correlation is the most common correlation observed in new drug applications. It represents a point-to-point relationship between in vitro drug dissolution and in vivo bioavailability of a drug from a dosage form[10-12].
Once IVIVC is established, it can guide the manufacturing process in many stages of drug product development. In addition, IVIVC can help set relevant in vitro dissolution specifications to ensure product quality[13,14]. Most significantly, when a level A IVIVC are established, the in vitro release method may be used as an alternative to measuring in vivo bioavailability. Thus, the conduct of in vivo studies may be reduced and the regulatory burden could be reduced[11,13,15].
Our goal was to determine the release profile of DOX from its matrix and to establish an IVIVC of four longacting DOX formulations with different proportions of acrylic acid polymer and polymethacrylate previously designed for oral administration in dogs[16].
Materials and Methods
DOX hyclate (Indukern, Mexico), polymethacrylate (Eudragit RL100®; Evonik, Germany) and acrylic acid polymer (Carbopol® 971 P NF polymer; Lubrizol, Mexico) were used in the present study.
Long-acting formulations (LAF):
Four different LAF were used, which according to our previous long-acting design[16], contained DOX hyclate, acrylic acid polymer, and polymethacrylate in the following ratios, DOX-LA1 (1:0.25:0.0035), DOX-LA2 (1:0.5:0.0075), DOX-LA3 (1:1:0.015), and DOX-LA4 (1:2:0.0225). After mixing, these formulations were granulated manually using the wet granulation process in ethanol. The granules were inserted in conventional gelatin capsules. Additionally, DOX without excipients was used as the control.
In vitro dissolution profile:
Dissolution tests were used to determine the velocity and quantity of a drug being released from the matrix. Because of materials cost, it was necessary to adapt a laboratory dissolution technique to obtain these data at lower cost while not sacrificing effectiveness. Thus, an experimental technique with continuous temperature and mixing was implemented, using an environmental shaker-incubator (Orbital SI-45) to maintain those conditions during a prolonged time. Dissolution profiles were obtained in two media: a phosphate buffer (PBS), pH of 7.4, and hydrochloric acid (HCl) 0.1 M with a pH of 1.3, to simulate gastrointestinal pH conditions in the dog.
LAFs and DOX were evaluated using 10 ml of each dissolution medium at a constant 37° temperature, maintained using a thermostatic bath and medium agitation (75 rpm). The release medium was replaced each time a sample was collected. Every sample was measured using a UV/Vis spectrophotometer (Varian Cary 1E, Spectralab Analytical) with ʎmaxof 270 nm.
Drug dissolution profiles were obtained by tiplicate from the absorbance data acquired at different times during a 60 h period using a calibration curve (absorbance versus drug concentration). A correction approach was included in the calculations to account for the drug being removed from the sampling. The cumulative percentage of drug release was plotted against time in order to obtain the release profile and calculate the in vitro dissolution data.
Model-dependent methods:
The values obtained from the dissolution study can be quantitatively analyzed by different methods of statistical comparisons (multivariate in most cases) that require fitting the dissolution curves to the equations or models that represent them. Table 1 presents the mathematical models with equations tested for fitting the experimental data.
| MODELS | PBS dissolution mediums | HCl Dissolution mediums | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DOX | DOX-LA1 | DOX-LA2 | DOX-LA3 | DOX-LA4 | DOX | DOX-LA1 | DOX-LA2 | DOX-LA3 | DOX-LA4 | |||
| Zero order F=k0×t | ||||||||||||
| K0 | 1.829 | 1.361 | 1.295 | 1.005 | 0.898 | 1.967 | 1.039 | 1.022 | 0.826 | 0.701 | ||
| R2 | 0.850 | 0.963 | 0.955 | 0.950 | 0.957 | 0.718 | 0.793 | 0.751 | 0.748 | 0.684 | ||
| AIC | 72.034 | 55.689 | 56.520 | 52.361 | 47.942 | 61.543 | 51.352 | 51.836 | 49.143 | 45.285 | ||
| First Order F=100×[1-Exp(-k1×t)] | ||||||||||||
| K1 | 0.040 | 0.021 | 0.020 | 0.014 | 0.012 | 0.048 | 0.014 | 0.014 | 0.010 | 0.008 | ||
| R2 | 0.951 | 0.963 | 0.961 | 0.979 | 0.975 | 0.965 | 0.907 | 0.882 | 0.843 | 0.787 | ||
| AIC | 61.813 | 55.619 | 54.931 | 43.887 | 43.135 | 46.302 | 44.976 | 45.943 | 45.343 | 41.763 | ||
| Higuchi F=kH×t0.5 | ||||||||||||
| Kh | 11.960 | 8.722 | 8.312 | 6.474 | 5.768 | 12.882 | 6.792 | 6.711 | 5.416 | 4.613 | ||
| R2 | 0.964 | 0.898 | 0.901 | 0.920 | 0.909 | 0.940 | 0.949 | 0.942 | 0.932 | 0.948 | ||
| AIC | 56.991 | 66.144 | 64.346 | 57.135 | 56.120 | 49.855 | 39.789 | 40.795 | 38.676 | 32.848 | ||
| Korsmeyer-Peppas F=kKP×tn | ||||||||||||
| Kkp | 8.278 | 1.957 | 2.813 | 2.316 | 1.916 | 8.486 | 3.003 | 3.087 | 2.372 | 3.055 | ||
| n | 0.602 | 0.921 | 0.805 | 0.775 | 0.817 | 0.713 | 0.731 | 0.750 | 0.722 | 0.704 | ||
| R2 | 0.984 | 0.963 | 0.976 | 0.982 | 0.983 | 0.893 | 0.931 | 0.900 | 0.889 | 0.936 | ||
| AIC | 51.903 | 58.004 | 52.527 | 44.437 | 41.749 | 57.472 | 47.223 | 47.080 | 44.324 | 35.824 | ||
| Hixon-Crowell F=100×[1-(1-kHC×t)3] | ||||||||||||
| KHc | 0.010 | 0.006 | 0.006 | 0.004 | 0.004 | 0.014 | 0.004 | 0.004 | 0.003 | 0.003 | ||
| R2 | 0.949 | 0.972 | 0.968 | 0.974 | 0.972 | 0.949 | 0.877 | 0.847 | 0.816 | 0.757 | ||
| AIC | 61.837 | 53.038 | 53.261 | 45.899 | 43.753 | 49.408 | 47.237 | 48.013 | 46.630 | 42.964 | ||
| Weibull F=100×{1-Exp[-((t-Ti)β)/α]} | ||||||||||||
| α | 11.312 | 46.779 | 32.002 | 39.141 | 43.908 | 22.167 | 33.386 | 35.627 | 42.883 | 47.695 | ||
| β | 0.747 | 1.007 | 0.875 | 0.830 | 0.811 | 0.919 | 0.812 | 0.823 | 0.813 | 0.713 | ||
| Ti | 0.933 | 0.800 | 0.933 | 0.800 | 0.800 | 0.800 | 0.800 | 0.800 | 0.800 | 0.800 | ||
| Td | 26.448 | 45.878 | 53.441 | 82.857 | 103.587 | 6.438 | 81.693 | 77.476 | 104.200 | 174.565 | ||
| R2 | 0.935 | 0.966 | 0.957 | 0.978 | 0.973 | 0.977 | 0.954 | 0.948 | 0.911 | 0.960 | ||
| AIC | 68.296 | 58.894 | 59.644 | 47.492 | 47.918 | 47.415 | 41.436 | 43.136 | 44.339 | 32.957 | ||
| Hopfenberg F=100×[1-(1-kHB×t)n] | ||||||||||||
| Khb | 0.011 | 0.008 | 0.009 | 0.004 | 0.004 | 0.013 | 0.004 | 0.004 | 0.003 | 0.003 | ||
| n | 2.667 | 2.333 | 2.000 | 3.000 | 3.000 | 3.667 | 3.375 | 3.000 | 3.000 | 3.000 | ||
| R2 | 0.949 | 0.975 | 0.970 | 0.974 | 0.972 | 0.964 | 0.880 | 0.961 | 0.816 | 0.757 | ||
| AIC | 63.811 | 54.040 | 54.673 | 47.899 | 45.753 | 48.763 | 49.027 | 50.013 | 48.630 | 44.964 | ||
| Peppas-Sahlin F=k1×tm+k2×t(2×m) | ||||||||||||
| k1 | 8.268 | 1.748 | 2.058 | 2.100 | 1.543 | 10.682 | 5.314 | 5.776 | 4.574 | 4.214 | ||
| k2 | 1.165 | 1.674 | 1.520 | 1.088 | 1.032 | 0.920 | 0.547 | 0.437 | 0.370 | 0.253 | ||
| m | 0.450 | 0.450 | 0.450 | 0.450 | 0.450 | 0.450 | 0.450 | 0.450 | 0.450 | 0.450 | ||
| R2 | 0.988 | 0.983 | 0.980 | 0.985 | 0.986 | 0.964 | 0.957 | 0.949 | 0.936 | 0.971 | ||
| AIC | 51.408 | 52.142 | 52.197 | 44.181 | 41.822 | 51.256 | 41.882 | 43.529 | 42.013 | 31.966 | ||
| Gompetz F=100×Exp{-α×Exp[-β×log(t)]} | ||||||||||||
| α | 6.032 | 8.001 | 6.651 | 5.792 | 5.676 | 7.765 | 5.176 | 5.151 | 5.105 | 4.743 | ||
| β | 1.963 | 1.704 | 1.518 | 1.194 | 1.096 | 2.274 | 1.161 | 1.151 | 1.002 | 0.837 | ||
| R2 | 0.881 | 0.916 | 0.910 | 0.950 | 0.939 | 0.943 | 0.987 | 0.991 | 0.967 | 0.988 | ||
| AIC | 72.633 | 66.123 | 65.533 | 54.129 | 54.259 | 52.855 | 30.714 | 27.801 | 34.424 | 23.157 | ||
| Logistic F=100×Exp[α+β×log(t)]/{1+Exp[α+β×log(t)]} | ||||||||||||
| α | -3.233 | -4.585 | -4.124 | -4.179 | -4.233 | -3.759 | -3.952 | -3.998 | -4.182 | -3.994 | ||
| β | 2.774 | 3.098 | 2.708 | 2.419 | 2.327 | 3.350 | 2.360 | 2.377 | 2.276 | 1.981 | ||
| R2 | 0.918 | 0.950 | 0.946 | 0.974 | 0.970 | 0.972 | 0.965 | 0.959 | 0.916 | 0.959 | ||
| AIC | 68.791 | 60.839 | 60.282 | 47.229 | 47.168 | 47.065 | 37.448 | 39.527 | 42.001 | 31.238 | ||
| Probit F=100×Φ[α+β×log(t)] | ||||||||||||
| α | -1.926 | -2.579 | -2.366 | -2.347 | -2.356 | -2.187 | -2.217 | -2.231 | -2.289 | -2.177 | ||
| β | 1.648 | 1.745 | 1.554 | 1.343 | 1.270 | 1.957 | 1.308 | 1.309 | 1.210 | 1.035 | ||
| R2 | 0.919 | 0.973 | 0.939 | 0.968 | 0.960 | 0.972 | 0.979 | 0.977 | 0.947 | 0.980 | ||
| AIC | 68.659 | 61.581 | 61.526 | 49.490 | 50.140 | 47.273 | 34.513 | 34.681 | 38.267 | 26.478 | ||
Results obtained using DDSolver software. K indicates a constant obtained for each model, n is dissolution constant, α is undissolved proportion at time and β is dissolution rate per unit of time
Table 1: Mathematical models of the long-acting DOX for PBS and HCL dissolution profile analysis
Several mathematical models have been postulated for fitting the percent-dissolved versus time data[17]. However, there is no universal model to fit all dissolution profiles and there are no established criteria to select the proper mathematical model[18]. To determine the suitable drug release kinetic model and the best-fitting equation, average data obtained for each product were fit with the statistical complement in Microsoft Excel DDSolver[19]. The values obtained for each model were evaluated with the coefficient of determination (R2) and Akaike’s Information Criterion (AIC). The best model is the one with the highest R2 and the one with the lowest AIC value[20].
Model-independent methods:
For the determination of dissolution data equivalence, FDA guidance[12] recommends approaches such as the model-independent approach, based on the calculation of difference (f1) and similarity (f2) factors, which provide a simple way to compare the data. These were calculated for all possible pairs of products considered. The f2 value was computed with the points of the dissolution profile up to the moment in which the product acting as reference in such comparison dissolved 85 % or more.
According to the FDA guidance the profiles were considered similar if f2 value was greater than or equal to 50 and f1 less than 15[12]. The f1 and f2 values were obtained with statistical complement of Microsoft Excel DDSolver[19]. In another model-independent method, DDSolver was used to calculate the values of area under the curve (AUC), mean dissolution time (MDT) and dissolution efficiency (DE). After obtaining those values for each formulation, they were statistically compared using ANOVAs[17,18].
In vivo study:
Forty-eight healthy adult dogs (2 to 8 y old) of different breeds and both sexes were included in this study. Their mean body weight was 17.75 kg (range, 15 to 30 kg), and all were vaccinated and determined to be healthy following physical examinations. The dogs were not medicated with any antibacterial medication for at least 30 d before the study, and during the study, all dogs received water ad libitum and were fed a commercial diet twice daily. This study was approved by the Institutional Subcommittee of Research, Care and Use of Experimental Animals according to the Mexican Official Regulation NOM-062-ZOO-1999. The study was carried out at the Facultad de Medicina Veterinaria of the Universidad Nacional Autónoma de México (UNAM), Mexico City. The owners of the dogs included in this study gave written consent for their dog's participation.
Study design:
In a crossover study, dogs were randomly assigned to one of 5 groups (4 experimental groups of 10 dogs each and a control group with 8 dogs) to receive a single oral dose (20 mg/kg) of DOX hyclate without excipients (control) or one of the four LAF. Animals received a dose of 20 mg of DOX/kg, which represents the cumulative dose for two days of treatment[1]. After administration, blood samples (3 ml) were obtained by venepuncture from each animal at 0, 1, 2, 4, 8, 12, 24, 36, 48, 60, 72 and 96 h after drug administration. The plasma was immediately separated from each sample by centrifugation and was stored at −20° until it could be analysed.
Plasma DOX concentration determination:
The plasma DOX concentrations were determined by modified agar diffusion analysis[21] with Bacillus cereus (ATCC 11778, American Type Culture Collection, Manassas, Va.) as a test organism on a Mueller-Hinton dehydrated growth medium (Bioxon, Becton Dickinson, Mexico City, Mexico). Drug concentrations were determined using linear regression analysis, comparing the diameters of the inhibition halos with the standard curve (200, 20, 10, 5, 2.5, 1.25, 0.625, 0.3125, and 0.1562 μg/ml) prepared in pooled antibacterial-free canine plasma.
Pharmacokinetic values:
To analyse plasma DOX concentration versus time curve for each individual dog after the oral administration of LAF, a computerized curve-stripping program (PKAnalyst, Micromath Scientific Software, Salt Lake City, United States) was used. And also AIC[20] and the graphical analysis of weighted residuals[22] were used to determine the optimal pharmacokinetic model. For oral administration, fitted DOX curves expressed the decrease in plasma drug concentration as a function of time and were approximated to one compartment with first-order input and first-order output.
Development of IVIVC:
Level A correlations are the point-to-point correlation between in vitro and in vivo profiles. They are generally considered to be the highest level of correlation and to allow prediction of the entire in vivo concentration time course from the in vitro dissolution profile[10]. IVIVC for DOX LAF was developed following the principles detailed in the USFDA IVIVC guidance on extended release oral dosage forms[12]. Absorbed drug fractions in in vivo profiles were obtained using the Wagner-Nelson method[23], and calculated as below: (XA)t/(XA)∞=(Cp+Kel (AUC0-t))/(Kel (AUC0-∞), where, Cp is the plasma concentration at time t, Kel is the elimination rate, AUC0-∞ is the area under the concentration-time curve from zero up to ∞ with extrapolation of the terminal phase. At each time point, the mean dissolved fraction (FD) was plotted versus the absorbed fraction (FA) calculated from the mean plasma concentration-time profile observed for each formulation[12]. The slope, intercept, and correlation coefficient describing the relationship between mean FD and FA were determined using linear regression. Standard errors in the IVIVC data were not shown because the average values were used.
IVIVC validation:
To validate the model, the mean in vitro dissolution data from formulations were used to calculate the predictable FA after the dose. This calculation was based on the IVIVC established with the in vitro dissolution and in vivo absorption correlation with linear regression for each formulation, FA = (slope)×FD±(intercept).
The first derivative of the predicted FA for matrix tablets was then used as the input rate for a onecompartment pharmacokinetic model with first-order elimination to simulate the expected plasma DOX concentration-time profile after an oral dose. The predicted plasma concentrations were obtained from the in vitro data by convolution using the IVIVC model; thereafter, the predicted and observed Cmax and AUC calculated by non-compartmental analysis were compared to calculate the prediction error (PE) by the following Eqn., PE (%) = (predicted value–observed value)/(observed value)×100.
Statistical analysis:
Data were reported as the mean±standard deviation (SD). Mean comparisons were made using multivariate ANOVA followed by the Tukey test. All results were obtained using SPSS statistical software (IBM SPSS statistics 20).
Results and Discussion
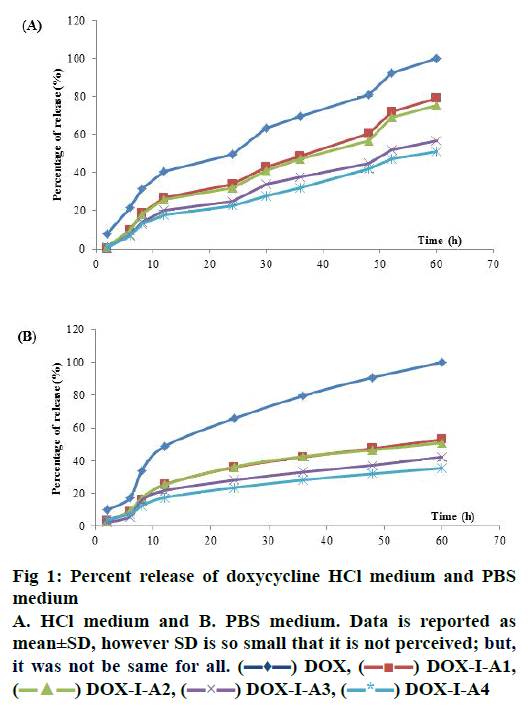
In the PBS medium, release profiles did not show statistical differences from 2 h until 48 h of dissolution. However, at the last point (60 h) DOX-LA2, DOXLA3 and DOX-LA4 did not show statistical differences between them and equally for DOX, DOX-LA1, DOX-LA2 and DOX-LA3 (p<0.05). Release curves for PBS medium are shown in fig. 1. All formulations were adjusted to many dissolution models, the fitting-equations and values obtained for each model are summarized in Table 1. According to values obtained for R2 and AIC, the best release profiles for all formulations in this medium could be explained by Peppas-Sahlin model, all values are summarized in Table 1. Based on this model, the fraction of drug release due to diffusion at a given point of time t can be calculated according this Eqn.[24], F = 1/(1+(K2/K1) t0.45). Thus, at hour 60 (last time-point) 64.78 % of the drug was released through diffusion mechanisms in DOX, and 60.6, 67.65, 66.18 and 72.52 % of the drug was released in DOX-LA1, DOX-LA2, DOX-LA3 and DOX-LA4, respectively.
The calculation of difference (f1) and similarity (f2) factors did not show similarity in any of the formulations. These data are summarized in Table 2. The AUC values obtained in PBS medium did not show statistical differences between LAFs. Values for MDT did not show any statistical difference between DOX, DOX-LA3 and DOX-LA4, nor between DOXLA1 and DOX-LA2. The values obtained for FD were statistically similar for DOX-LA1 and DOX-LA2, and for DOX-LA3 and DOX-LA4 (p<0.05). Data are summarized in Table 3.
| Dissolution mediums | PBS | HCl | |||||
|---|---|---|---|---|---|---|---|
| Possible comparisons | f1 | f2 | Similarity | f1 | f2 | Similarity | |
| DOX | DOX-LA1 | 86.12 | 15.37 | NO | 47.70 | 25.94 | NO |
| DOX-LA2 | 101.50 | 14.15 | NO | 48.06 | 25.64 | NO | |
| DOX-LA3 | 74.44 | 18.24 | NO | 58.09 | 21.53 | NO | |
| DOX-LA4 | 92.9 | 46.02 | NO | 46.66 | 19.25 | NO | |
| DOX-LA1 | DOX-LA2 | 82.95 | 21.15 | NO | 2.39 | 93.54 | YES |
| DOX-LA3 | 148.97 | 14.43 | NO | 19.86 | 57.63 | YES* | |
| DOX-LA4 | 118.14 | 19.33 | NO | 31.17 | 47.84 | NO | |
| DOX-LA2 | DOX-LA3 | 68.61 | 22.87 | NO | 19.31 | 58.89 | YES* |
| DOX-LA4 | 104.48 | 19.02 | NO | 31.14 | 48.63 | NO | |
| DOX- LA3 | DOX-LA4 | 61.32 | 25.27 | NO | 17.14 | 67.55 | YES* |
Results obtained using DDSolver software. *Indicates that similarity was established only by one of the factors
Table 2: Difference (f1) and similarity (f2) factors for release profiles of DOX and long-acting formulation in PBS and HCL dissolution mediums
| PBS dissolution mediums | |||||||
|---|---|---|---|---|---|---|---|
| DOX | DOX-LA1 | DOX-LA2 | DOX-LA3 | DOX-LA4 | |||
| Mean±SD | Mean±SD | Mean±SD | Mean±SD | Mean±SD | |||
| AUC | 3598±219 | 2548.14a±122 | 2431.28a±98 | 1910.69b±89 | 1695.58b±98 | ||
| MDT | 24.02a±2.19 | 27.83b±0.90 | 27.75b±1.54 | 26.30ab±0.59 | 26.83ab±0.88 | ||
| DE | 0.60±0.04 | 0.42a±0.02 | 0.41a±0.02 | 0.32b±0.01 | 0.28b±0.02 | ||
| HCl dissolution mediums | |||||||
| AUC | 4008.4±332 | 2118.60a±312 | 2104.57a±443 | 1684.35a±153 | 1434.79a±291 | ||
| MDT | 19.92a±3.32 | 20.09a±1.66 | 18.91a±2.22 | 20.23a±2.21 | 19.85a±3.04 | ||
| DE | 0.67±0.06 | 0.35a±0.05 | 0.35a±0.07 | 0.28a±0.03 | 0.24a±0.05 | ||
AUC=area under de curve; MDT=mean dissolution time; DE=dissolution efficiency. Data were obtained by DDSolver software. a-b Within a row, the values without a common superscript letter differ significantly (p<0.05)
Table 3: Pharmacokinetic values obtained for DOX and DOX long-acting formulations release profiles in PBS and HCL dissolution mediums
The HCl medium showed statistical differences at all sample times. At 2 and 6 h LAFs did not show statistical differences between each other, but they were all different from DOX. DOX-LA1 and DOXLA2 did not show statistical differences at h 8, 12, 24 and 48, similarly to DOX-LA3 and DOX-LA4, but these were all different to DOX. At h 30 and 36, DOXLA1 and DOX-LA2 were not statistically different, and neither were DOX-LA3 and DOX-LA4, nor DOXLA1 and DOX-LA2 at h 52 and 60. Release curves for HCl medium are shown in fig. 1. In the dependentmodel methods, all formulations were adjusted to many dissolution models. The Weibull Eqn. provided the best mathematical fit for DOX, while the Gompetz model best fit the other formulations. All values are summarized in Table 1. The calculation of difference (f1) and similarity (f2) factors showed similarity between DOX-LA1 and DOX-LA2; however, considering only f2 factor DOX-LA3 might be similar to DOXLA1, DOX-LA2 and DOX-LA4. All these data are summarized in Table 2.
The values obtained for AUC and ED in HCl medium did not show statistical differences between LAFs, although DOX differed from the rest. MDT values did not show any statistical difference between any formulations (p<0.05). Data are summarized in Table 3.
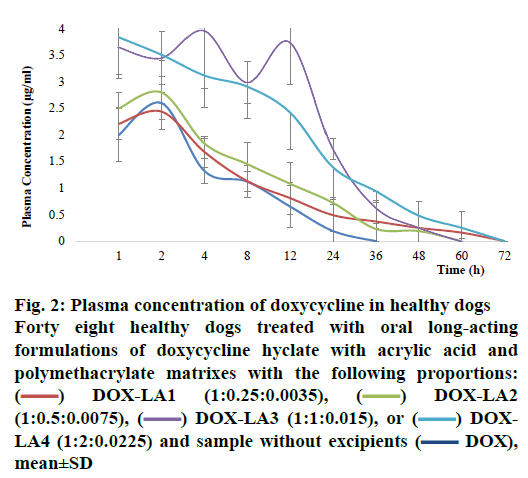
The pharmacokinetic values for all formulations are summarized in Table 4. Comparisons of Cmax, retention time, AUC, AUC0–∞, K½el and Kel between all treatments revealed that these parameters did not differ statistically between DOX-LA1, DOX-LA2 and DOX, but these three formulations differed significantly from DOX-LA3 and DOX-LA4 (p<0.05). The dogs that received DOX-LA1 and DOX-LA4 had detectable plasma DOX concentrations 60 h post-administration, while the dogs treated with DOX-LA2 and DOX-LA3 only had detectable plasma concentrations for 48 h after administration. The 4 LAFs lasted longer than did the control treatment, which only led to 24 h of detectable DOX concentrations in plasma (fig. 2). However, DOX-LA4 showed higher concentrations for 60 h compared with DOX-LA1, and DOX-LA3 had higher concentrations during 48 h, compared to DOX-LA2.
| Mean ± SE | DOX (without excipients) | DOX-LA1 (1:0.25:0.0037) |
DOX-LA2 (1:0.5:0.0075) | DOX-LA3 (1:1:0.015) |
DOX-LA4 (1:2:0.0225) |
|---|---|---|---|---|---|
| K½el (h) | 7.54±0.17a | 8.5±0.46a | 12.02±0.92a | 17.36±0.4b | 15.21±0.9b |
| Cmax (µg/ml) | 2.6±0.28a | 2.63±0.106a | 2.41±0.88a | 4.11±0.21b | 4.11±0.21b |
| AUC (µg×h/ml) | 22.1±2.52a | 32,46±0.66a | 41.57±3.08a | 106.4±4.5b | 88.6±5.05b |
| AUC∞ (µg×h/ml) | 24.18±2.5a | 34.54±0.75a | 45.11±3.42a | 112.7±4.4b | 94.04±5.4b |
| RT (h) | 10.82±0.3a | 12.37±0.66a | 17.34±1.33a | 25.26±0.6b | 22.01±1.4b |
| Kel (h-1) | 0.09±0.002a | 0.08±0.004a | 0.06±0.006b | 0.04±0.001b | 0.05±0.003b |
a-bValues within a row, with no common superscript differ significantly (p<0.05). K½el = elimination half rate; Cmax is calculated maximum plasma concentration; AUC is area under the curve; AUC∞ is area under the concentration-time curve from zero up to ∞ with extrapolation of the terminal phase; RT is retention time and Kel is elimination rate. Data expressed as mean±standard error (SE)
Table 4: Pharmacokinetic data obtained after oral administration of long-acting formulations of doxycycline in healthy dogs. Data is expressed in mean ± standard error (SE)
Figure 2: Plasma concentration of doxycycline in healthy dogs
Forty eight healthy dogs treated with oral long-acting formulations of doxycycline hyclate with acrylic acid and polymethacrylate matrixes with the following proportions:  DOX-LA1 (1:0.25:0.0035),
DOX-LA1 (1:0.25:0.0035),  DOX-LA2 (1:0.5:0.0075),
DOX-LA2 (1:0.5:0.0075),  DOX-LA3 (1:1:0.015), or
DOX-LA3 (1:1:0.015), or  DOXLA4 (1:2:0.0225) and sample without excipients (
DOXLA4 (1:2:0.0225) and sample without excipients ( DOX), mean±SD
DOX), mean±SD
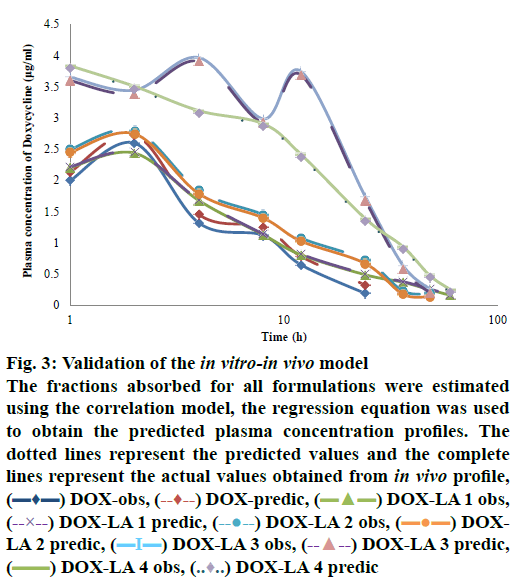
The level A IVIVC was confirmed with the coefficient of correlation (R2) obtained by plotting the in vitro and in vivo profiles of each formulation. A one-to-one linear relationship between the fractions released in vitro and fractions released/absorbed in vivo was observed (DOX, DOX-LA1 and DOX-LA2 R2>0.9581 and DOX-LA3 and DOX-LA4 R2>0.999). To validate the model, the fractions absorbed for all formulations were estimated using the correlation model; then regression Eqns. were used to obtain the predicted plasma concentration profiles as shown in fig. 3. PEs (%) at each time point were lower than 6 % for DOX-LA1 and lower than 14 % for DOX-LA4, while DOX, DOX-LA2 and DOXLA3 showed PE lower that 8.9 % at all-time points, except at 60 h, when all three formulations showed PE between 20 and 26 %. Finally, PE for Cmax and AUC0-∞ values were calculated and are summarized in Table 5. The percent error between predicted and real values was lower than 15 % in all formulations. Eqns. to obtain the predictions are summarized in Table 5. As shown in fig. 3, all predicted in vivo release profiles were almost identical to the experimental in vivo release profiles. These results confirmed that the developed IVIVCs were sufficiently robust.
Figure 3: Validation of the in vitro-in vivo model
The fractions absorbed for all formulations were estimated using the correlation model, the regression equation was used to obtain the predicted plasma concentration profiles. The dotted lines represent the predicted values and the complete lines represent the actual values obtained from in vivo profile,  DOX-obs,
DOX-obs,  DOX-predic,
DOX-predic,  DOX-LA 1 obs,
DOX-LA 1 obs,  DOX-LA 1 predic,
DOX-LA 1 predic,  DOX-LA 2 obs,
DOX-LA 2 obs,  DOXLA 2 predic,
DOXLA 2 predic,  DOX-LA 3 obs,
DOX-LA 3 obs,  DOX-LA 3 predic,
DOX-LA 3 predic,  DOX-LA 4 obs,
DOX-LA 4 obs,  DOX-LA 4 predic
DOX-LA 4 predic
| Formulation | Cmax (µg/ml) | AUC (µg×h/ml) | Equations | ||||
|---|---|---|---|---|---|---|---|
| Observed | Predicted | PE % | Observed | Predicted | PE % | ||
| DOX | 2.6 | 2.73 | 5 | 24.18 | 23.88 | 1.24 | FD = 1.1419(FA)-0.1555 |
| DOX-LA1 | 2.63 | 2.45 | 6.84 | 32.46 | 36.81 | 13.41 | FD = 3.2707(FA)-0.0343 |
| DOX-LA2 | 2.41 | 2.74 | 13.69 | 41.57 | 36.79 | 11.50 | FD = 0.3882(FA)+0.0197 |
| DOX-LA3 | 4.11 | 3.91 | 4.86 | 106.35 | 90.10 | 15.28 | FD = 0.5004(FA)+0.0287 |
| DOX-LA4 | 4.11 | 3.8 | 7.54 | 88.6 | 82.51 | 6.87 | FD = 0.5498(FA)+0.0201 |
PE (%) represents the percent error between actual and predicted values; FD is fraction dissolved; and FA is fraction absorbed. The predictive ability of the IVIVC was examined by using the IVIVC developed with use of long-acting formulation to predict the plasma concentration-time
Table 5: Validation and prediction data for Cmax and AUC values according to the established in vitro/in vivo correlation model
According to the Biopharmaceutical Classification System (BCS), DOX is a class I drug that presents high solubility and high permeability. The drug should also be chemically stable for 24 h over this same pH range. In addition to these, DOX exhibits more than 80 % bioavailability[25]. There are no rate-limiting steps for drug absorption for class 1 compounds, with the possible exception of immediate release dosage forms, for which gastric emptying could potentially become the rate-limiting step[11,26].
The pharmaceutical formulations of DOX was designed to remain in the upper portion of the gastrointestinal tract (stomach or duodenum) in order to increase bioavailability[1] and to protect from adverse reactions[5-7]. Retention of the pharmaceutical dosage form in the desired portion of the gastrointestinal tract can be achieved by delaying the dosage form expulsion from the gastrointestinal tract using techniques such as bio adhesion, flotation, swelling, or a combination thereof[8]. It is not clear whether release of the longacting DOX formulation used here occurs completely in the intestine and/or in the stomach environment, thus both PBS and HCl dissolution profiles were performed.
Mathematical models were used to adjust dissolution data because they facilitate the analysis and interpretation of observed data by describing the dissolution profiles as a function of only a few model parameters that can be compared statistically[27].
The behaviour of DOX release in LAF and without excipients in PBS medium was mainly explained by Peppas-Sahlin[24]. This semi-empirical model describes drug release from polymeric systems. It accounts for the coupled effects of Fickian diffusion and case II transport[28]. The K1 values indicate the diffusion (Fickian diffusion) contribution, while K2 values are associated with dissolution as well as relaxation of polymer chains (erosion). If K1 and K2 values are available, the percent of drug release due diffusion can be calculated[28,29]. Both K1 and K2 values decreased with increasing excipient concentration. Thus, according to the values obtained with Eqn. F, the percentage of drug released by diffusion process increased as the excipients increased.
The diffusion exponent value in the power law indicated a non-Fickian mechanism of drug release; however, the drug dissolution occurring via Fickian diffusion proved to be essential because the K1 diffusion constant is much higher than the K2 relaxation rate constant[17]. Nonetheless, the Fickian contribution to the whole release process decreased with increasing the amount of drug release, hence the relaxation of the polymer chains became more pronounced. The higher K1 than K2 value, indicates that Fickian diffusion was the predominant mechanism of drug release from the matrices, rather than polymer relaxation and swelling in the matrix[28,29].
Calculation of the approximate contribution and coupled effect of Fickian diffusion and polymer relaxation mechanisms to an anomalous release process based on logic concepts was carried out by fitting the data to the heuristic approach proposed by Peppas and Sahlin[24] to quantify and materialize the amount of drug released by the two phenomena controlling the drug release from swellable matrix.
According to the calculated diffusion exponents for all formulations (except DOX-LA1) using power laws, non-Fickian diffusion is the principal release mechanism. This indicates an anomalous mechanism transport, best described by a combination of diffusion and swelling (macromolecular relaxation processes) controlled release mechanism[24]. It also indicates that drug release was highly influenced by swelling and gradual matrix erosion. We concluded that carbopol and Eudragit-RL100 forms a gel which swells and erodes, which in turn resulted in the typical release mechanism of non-Fickian diffusion.
Release in the HCl medium best fit the Weibull model for DOX, and the Gompetz model best fit the other formulations. The geometric shape of the tablet diminishes proportionally over time. It is assumed that release-rate is limited by the dissolution rate of drug particles[17,30]. Although the Weibull distribution cannot adequately characterize the dissolution kinetic properties of the drug, it can describe the dissolution curve in terms of applicable parameters. An advantage of this model is that parameter calculation is independent of whether or not sink conditions prevail. As the reference was well adjusted to this function, β parameter was used to compare the dissolution profiles. The Weibull shape parameter β characterizes the curve of the dissolution profile as exponential (β =1); as sigmoid S-shaped, with upward curvature followed by a turning point (β>1); or as parabolic, with a steeper initial slope that is consistent with the exponential (β<1)[17,30]. For DOX β value is lower than one (β<1), it showed that the release occurs in exponential way.
The time parameter, Td, can be calculated from α and β parameters and represents the time interval necessary to dissolve 63.2 % of the drug[17,30]. According to this parameter, DOX required 6.4 h to dissolve 63.2 % in all formulations, and the time of dissolution increased considerably with the rise of the excipient proportion. A higher Td value indicates slower release.
In the Gompetz model, the α value determines the undissolved proportion at each time and β represents the dissolution rate per unit of time as a shape parameter. In the long-acting formulation, β decreased with excipient increase. It is a type of mathematical model for a time series, where release rate is slowest at the start and end of a time period. This model has a steep increase in the beginning and converges slowly to the asymptotic maximal dissolution[30].
The f1 and f2 factors estimate the percent difference between the two curves and the relative error between them. The comparison of values such as MDT, AUC and DE contribute information to clarifying the release mechanism and should be used in association with each other or with some of the models previously mentioned[17].
In the present study, DOX-LA1 and DOX-LA4 were clinically efficacious for 60 h, but DOX-LA4 showed almost double the Cmax value compared to DOX-LA1. Similar data were obtained with DOXLA2 and DOX-LA3, both with biological effects during 48 h, but the Cmax of DOX-LA3 is higher than DOX-LA2. Nevertheless, DOX is a time-dependent drug, meaning it is not necessary to have huge peaks when the concentration is over the MIC specific for the microorganism being treated[3]. DOX shows the best clinical efficacy at low concentrations, 2 to 4 times the MIC, in this case the inhibition of the microorganisms occurs in a time-dependent way. At higher concentrations, 8 to 16 times the MICs of the microorganism treated, DOX exhibited concentrationdependent killing[4]. Higher plasma concentrations were obtained with DOX-LA4, however, being a timedependent drug, it is not necessary to have huge peaks while the concentration maintained over the MIC specific for the microorganism treated, and that effect was obtained with DOX-LA1.
For the IVIVC, the PBS was used in vitro values, considering that in vivo the drug was probably retained for more time in the intestinal environment. In our correlation all the predicted in vivo release profiles were almost identical to the experimental in vivo release profiles in dogs. These results confirmed that the developed IVIVCs were sufficiently robust. Most importantly, the developed IVIVCs can be used to predict not only the DOX matrix formulations that are equivalent in formulation composition but also those matrixes formulations that are not equivalent in composition but with similar drug loading. With the IVIVC application, in vivo drug performance can be predicted from its in vitro behaviour. The establishment of a meaningful IVIVC can provide a surrogate for bioequivalence studies, improve product quality, and reduce regulatory burden[11,13].
For all formulations, the PE between predicted values and actual values are lower than 15 %. Considering that the FDA acceptance criteria guidelines indicate that if the average of the absolute % PE is 10 % or less for Cmax and AUC, this establishes a good prediction level. Moreover, % PE should not exceed 15% in any formulation[12].
The ability of the IVIVC to accurately predict the observed plasma concentration-time profile of these LAFs supports the assertion that the in vitro dissolution of DOX in this dosage form is closely related to the in vivo fraction absorbed. These studies support the idea that an IVIVC for high-solubility, high-permeability drugs, such as DOX, will be observed when dissolution is the rate-limiting step in absorption.
The results from this IVIVC study should not be fully extrapolated to humans since there are known differences in drug absorption and drug release between dogs and humans. A similar study performed with human pharmacokinetics data would be necessary for an IVIVC to be fully applicable to human drug products.
Acknowledgements:
Authors wish to thank PAFFA Laboratories in Mexico for financial support for this project. Additionally we acknowledge Gabriela Rocha, a chemistry student, for her participation in experimental procedures.
Conflict of interest:
The authors report no conflicts of interest regarding this work. The authors alone are responsible for the content and writing of the paper.
References
- Holmes N, Charles P. Safety and efficacy review of doxycycline. Clin Med Insights Ther 2009;1:471-82.
- Lee H, Park JW, Kim SP, Lo EH, Lee SR. Doxycycline inhibits matrix metalloproteinase-9 and laminin degradation after transient global cerebral ischemia. Neurobiol Dis 2009;34:189-98.
- Zeng S, Zhou X, Tu Y, Yao M, Han ZQ, Gao F, et al. Long-Term MMP inhibition by doxycycline exerts divergent effect on ventricular extracellular matrix deposition and systolic performance in stroke-prone spontaneously hypertensive rats. Clin Expl Hypertens 2011;33:316-24.
- Cunha BA, Domenico P, Cunha CB. Pharmacodynamics of doxycycline. Clin Microbiol Infec 2000;6:270-3.
- Riond JL, Riviere J. Doxycycline binding to plasma albumin of several species. J Vet Pharmacol Ther 1988;12(3):253-60.
- Smith K, Leyden JJ. Safety of doxycycline and minocycline: a systematic review. Clin Ther 2005;27:1329-342.
- Xiao SY, Zhao L, Hart J, Semrad CE. Gastric mucosal necrosis with vascular degeneration induced by doxycycline. Am J Surg Pathol 2013;37:259-63.
- Shen S, Jasti B, Li X. Design of controlled-release drug delivery systems. In: Kutz M, editor. Standard Handbook of biomedical Engineering & Design. New York: McGraw-Hill; 2003. p 161-79.
- Uhrich KE, Cannizzaro SM, Langer RS, Shakesheff KM. Polymeric Systems for Controlled Drug Release. Chem Rev 1999;99(11):3181-98.
- Cardot JM, Beyssac E, Alric M. In vitro-in vivo correlation Importance of dissolution in IVIVC. Dissolut Technol 2007;14:15-19.
- Lu Y, Kim S, Park K. In vitro-in vivo correlation: Perspectives on model development. Int J Pharm 2011;418:142-8.
- FDA. Guidance for Industry Extended Release Oral dosage Forms: Development, Evaluation, and Application of in vitro/in vivo Correlations, U.S. Department of Human Health and Human Services, Food and Drug Administration. 1997. Available from: https://www.fda.gov/regulatory-information/search-fda-guidance-documents/extended-release-oral-dosage-forms-development-evaluation-and-application-vitroin-vivo-correlations
- Emami J. In vitro-in vivo correlation: from theory to applications. J Pharm Pharm Sci 2006;9:169-89.
- Roudier B, Davit BM, Beyssac E, Cardot JM. In vitro-in vivo correlation's dissolution limits setting. Pharm Res 2014;31:2529-38.
- Young D. In vitro-in vivo correlation for modified release parenteral drug delivery systems. In: Chilukuri DM, Sunkura G, Young D, editors. Pharmaceutical Product Development: In vitro–in vivo Correlation. New York: Informa Healthcare; 2000. p 141-51.
- Arciniegas-Ruiz SM, Gutiérrez-Olvera L, Bernad-Bernad MJ, Caballero-Chacón Sdel C, Vargas-Estrada D. Comparative pharmacokinetics of a new oral long-acting formulation of doxycycline hyclate: A canine clinical trial. Eur J Pharm Sci 2015;80:9-15.
- Costa P, Sousa Lobo JM. Modeling and comparison of dissolution profiles. Eur J Pharm Sci 2001;13:123-33.
- Shah JC, Deshpande A. Kinetic modeling and comparison of in vitro dissolution profiles. World J Pharm Sci 2014;2:302-309.
- Zhang Y, Huo M, Zhou J, Zou A, Li W, Yao C, et al. DDSolver: An Add-In Program for Modeling and Comparison of Drug Dissolution Profiles. AAPS J 2010;12:263-71.
- Burnham KP, Anderson DR. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol Method Res 2004;33:261-304.
- Okerman L, Croubels S, Cherlet M, De Wasch K, De Backer P, Van Hoof J. Evaluation and establishing the performance of different screening tests for tetracycline residues in animal tissues. Food Addit Contam 2004;21(2):145-53
- Gabrielsson J, Weiner D. Parameter estimation. In: Gabrielsson J, Weiner D, editors. Pharmacokinetic and pharmacodynamic data analysis, concepts and applications. 4th ed. Sweden: Swedish Pharmaceutical Press; 2007. p. 21-44.
- Banker G, Rhodes C. Modern pharmacokinetics. 4th ed. New York: Marcel Deker Inc., Taylor and Francis group; 2002. p. 124-8.
- Peppas A, Sahlin JJ. A simple equation for the description of solute release. III. Coupling of diffusion and relaxation. Int J Pharm 1989;57:169-172.
- Agwuh KN, MacGowan A. Pharmacokinetics and pharmacodynamics of the tetracyclines including glycylcyclines. J Antimicrob Chemother 2006;58:256-65.
- Modi NB. In vitro-in vivo correlation. In: Chilukuri DM, Sunkara G, Young SG, editors. Pharmaceutical Product Development. New York: Informa Healthcare; 2007. p. 107-23.
- Adams E, Coomans D, Smeyers-Verbeke J, Massart DL. Non-linear mixed effects models for the evaluation of dissolution profiles. Int J Pharm 2002;240:37-53.
- Mady OY. Mechanisms and percent of drug release of each new mathematic approach. Int Res J Pharm Appl Sci 2013;3:56-69.
- Siepmann J, Peppas NA. Modeling of drug release from delivery systems based on hydroxypropyl methylcellulose (HPMC). Adv Drug Deliv Rev 2001;48:139-57.
- Ramteke KH, Dighe PA, Kharat AR, Patil S. Mathematical Models of Drug Dissolution: A Review. Scholars Acad J Pharm 2014;3:388-96.
 DOX,
DOX,  DOX-I-A1,
DOX-I-A1,  DOX-I-A2,
DOX-I-A2,  DOX-I-A3,
DOX-I-A3,  DOX-I-A4
DOX-I-A4