P. C. Sharma*, S. V. Sharma1, Archana sharma and B. Suresh2

University institute of pharmaceutical sciences, Kurukshetra university, Kurukshetra-136 119, India
1School of chemical sciences and pharmacy, university of east anglia, Norwich, NR47TJ, UK
2J. S. S. college of pharmacy, Rocklands, Ootacamund-643 001, India

*Corresponding Author:
P. C. Sharma
University institute of pharmaceutical sciences, Kurukshetra university, Kurukshetra-136 119, India
E-mail: sharma_prabodh@rediffmail.com
Date of Submission 11 December 2006
Date of Revision 14 January 2008
Date of Acceptance 1 March 2008
Indian J Pharm. Sci, 2008, 70 (2): 154-158  

DOI: 10.4103/0250-474X.41447

Abstract

A three dimensional quantitative structure-activity relationship study using the comparative molecular field analysis method was performed on a series of 3-aryl-4-[α-(1H-imidazol-1-yl) aryl methyl] pyrroles for their anticandida activity. This study was performed using 40 compounds, for which comparative molecular field analysis models were developed using a training set of 33 compounds. Database alignment of all 33 compounds was carried out by root-mean-square fit of atoms and field fit of the steric and electrostatic molecular fields. The resulting database was analyzed by partial least squares analysis with cross-validation; leave one out and no validation to extract optimum number of components. The analysis was then repeated with bootstrapping to generate the quantitative structure-activity relationship models. The predictive ability of comparative molecular field analysis model was evaluated by using a test set of 7 compounds. The 3D- quantitative structure-activity relationship model demonstrated a good fit, having r 2 value of 0.964 and a cross validated coefficient r 2 value as 0.598. Further comparison of the coefficient contour maps with the steric and electrostatic properties of the receptor has shown a high level of compatibility and good predictive capability.

Keywords

CoMFA, 3D-QSAR, Pyrroles, Anticandida activity

Fungal infections in the human, range from superficial and cutaneous (such as dermatomycosis) to deeply invasive and disseminated (such as candidiasis and cryptococcosis) infections. In the past 20 years, fungal infections have increased dramatically-paradoxically, as risk advances. Fungal infections occur more frequently in people whose immune system is suppressed (because of organ transplantation, cancer chemotherapy, or the acquired immune deficiency syndrome) or who have been subject to invasive procedures (catheters, prosthetic device) [1]. Fungal infections are now important causes of morbidity and mortality among immuno-compromised hospitalized patients. The frequency of invasive candidiasis has increased ten-fold during the past decade [2].

Candida albicans (CA) has been identified as the major opportunistic pathogen in the etiology of fungal infections; however, the frequency of other Candida species is increasing [3]. The current standard of therapies is the fungicidal (but toxic) polyene antibiotic, amphotericin B, and the safer (but fungistatic) azoles. In particular, the latter class of drugs is an important antifungal class widely used for AIDS-related mycotic pathologies [4].

Quantitative structure activity relationship (QSAR) enables the investigators to establish a reliable quantitative structure-activity and structure-property relationships to derive in silico QSAR models to predict the activity of novel molecules prior to their synthesis. The overall process of QSAR model development can be divided into three stages namely, data preparation, data analysis, and model validation, representing a standard practice of any QSAR modeling. Successful application of 3D-QSAR methodologies have been used to generate models for various chemotherapeutic agents [5,6].

We have carried out 3D-QSAR studies employing comparative molecular field analysis [5] (CoMFA) techniques in order to study and gain further insight to deduce a correlation between structure and biological activity of 3-aryl-4-[α-(1H-imidazol-1-yl) aryl methyl] pyrroles as potent anticandida agents [7].

In the CoMFA method, introduced by Crammer [8,9], a relationship is established between the biological activities of a set of compounds and their steric and electrostatic properties. An advantage of CoMFA is its ability to predict the biological activity of molecules and represent the relationship between steric and electrostatic properties and biological activity in the form of contour maps [10]. An ‘active conformation’ of the ligands is generated and superimposed as per the predefined rules. These molecules are then placed in a box of predefined grid size. The steric and electrostatic interaction energy between each structure and a probe atom of defi ned size and charge are calculated at each grid point using the molecular mechanics force fields. A multivariate data analysis technique like partial least squares (PLS) [11-13] is used to derive a linear equation from the resulting matrices. PLS is used in combination with cross validation to obtain the optimum number of components. This ensures that the QSAR models are selected on their ability to predict the data rather than to fit the data. The advantages of CoMFA studies are in the ability to predict the target properties of the compounds and to graphically present the QSAR in the form of coefÞ cient contour maps [14].

We present here 3D-QSAR studies using CoMFA method on a series of 3-aryl-4-[α-(1H-imidazol-1-yl) aryl methyl] pyrroles and the contour maps derived reveal the significance of steric and electrostatic fields. The structural variations in the molecular fields at particular regions in the space provide underlying structural requirements and 3D-QSAR models generated give good predictive ability and aid in the design of potent anticandida agents.

Materials and Methods

Biological activity data

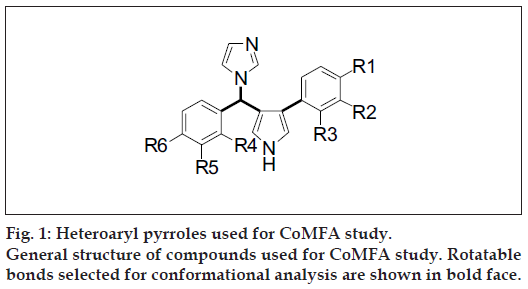
The antifungal activity data against Candida albicans for a series of 3-aryl-4-[α-(1H-imidazol-1-yl) aryl methyl] pyrroles containing 40 compounds as anticandida agents was used in this analysis. General structure of the compounds is shown in (fig. 1). Training set was formed by selecting 33 compounds from the original series. Test set compounds were no. 11, 12, 33, 34, 35, 37 and 42 (total 7 compounds), selected randomly. These compounds were not included in the analysis to generate the CoMFA model. The robustness and predictive ability of models were evaluated by selecting biological activity with chemical class similar to training set. CoMFA techniques were used to derive 3D-QSAR models for 3-aryl-4-[α-(1Himidazol- 1-yl)aryl methyl)pyrroles. The MIC data were used for the QSAR analysis as a dependent parameter, after converting to the reciprocal of the logarithm of MIC (pMIC) expressed in μM/ml (Table 1).

Figure

Figure 1: Heteroaryl pyrroles used for CoMFA study. General structure of compounds used for CoMFA study. Rotatable bonds selected for conformational analysis are shown in bold face.

Compd No. R1 R2 R3 R4 R5 R6 MIC µg/ml MIC µM/ml pMIC
1 H H H H H H 53.9 0.180 0.744
2 H H H H H Cl 47.3 0.142 0.847
3 H H H H H F 71.2 0.224 0.648
4 H H H H H CH3 133.3 0.425 0.370
5 H H H H H NO2 56.7 0.164 0.782
6 H H H H H NH2 142.4 0.453 0.343
7 H H Cl H H H 43.8 0.130 0.885
8 H H Cl H H Cl 18.7 0.050 1.292
9 H H Cl H H F 48.3 0.137 0.861
10 H H Cl H H CH3 35.4 0.102 0.991
11* H H Cl H H NO2 50.7 0.134 0.8722
12* H H Cl H H NH2 100.4 0.288 0.539
13 H H Cl Cl H Cl 5.19 0.012 1.887
14 H H Cl H Cl Cl 13.8 0.034 1.463
15 Cl H H H H H 12.8 0.038 1.415
16 Cl H H H H Cl 12.3 0.033 1.474
17 Cl H H H H F 15.4 0.043 1.357
18 Cl H H H H CH3 12.3 0.035 1.450
19 Cl H H H H NO2 60.12 0.159 0.798
20 Cl H H H H NH2 42.8 0.122 0.910
21 Cl H H Cl H Cl 3.94 0.009 2.007
22 Cl H H H Cl Cl 14.4 0.035 1.444
23 Cl H Cl H H H 8.4 0.022 1.640
24 Cl H Cl H H Cl 6.8 0.016 1.770
25 Cl H Cl H H F 7.8 0.020 1.693
26 Cl H Cl H H CH3 7.9 0.020 1.683
27 Cl H Cl H H NO2 22.9 0.055 1.255
28 Cl H Cl Cl H Cl 7.4 0.017 1.769
29 Cl H Cl H Cl Cl 7.2 0.016 1.781
30 Cl Cl H H H H 7.2 0.019 1.707
31 Cl Cl H H H Cl 8.9 0.022 1.653
32 Cl Cl H H H F 7.2 0.018 1.744
33* Cl Cl H H H CH3 7.9 0.020 1.683
34* Cl Cl H Cl H Cl 5.9 0.013 1.867
35* Cl Cl H H Cl Cl 2.2 0.021 1.677
36* H H H H Cl Cl 38.6 0.103 0.987
37 H H H H H 1pyrrole 30.4 0.081 1.091
38 H H Cl H H 1pyrrole 20.5 0.051 1.292
39 Cl H H H H 1pyrrole 119 0.29 0.537
40* Cl H Cl H H 1pyrrole 33.7 0.078 1.107

Table 1: Experimental activities of molecules used in training set and test set

Molecular modeling

A database of 33 compounds forming the training set was generated by molecular modeling. All molecular modeling and 3D-QSAR studies were performed using SYBYL 6.7 [15] with TRIPOS Force Field [16] on a Silicon Graphics O2 workstation with IRIX operating system. The crystallographic data for these ligand complexes was not available hence all the molecules were constructed using a grid having a spacing of 1.54 A0 between grid points. This is the default spacing, which represents sp3 carboncarbon bond length. The molecules were cleaned up and quick minimized after sketching. Because no experimental data on the biologically relevant conformations of the selected compounds were available (for example, atomic coordinates derived from X-ray crystallographic studies of their complexes with the putative receptor), we resorted to a general molecular mechanics approach (AM1) to build the conformational models to be used for generation of CoMFA models. A chirality check was performed to identify chiral atoms, after adding hydrogens, it was important to consider all possible enantiomers as the activity was reported for racemic mixtures. Then the molecules were subjected for energy minimization (geometry optimization) at a gradient of 1.0 kcal/mol with delta energy change of 0.001 kcal/mol with the TRIPOS standard force Þ eld. Structures were drawn by using default setting of SYBYL.

After conformational analysis (CA) by adopting AM1 Hamiltonian approach, the least energy conformation was selected, saved, and used for the charge calculation, assuming that it was the active one. We have used two different types of charges, calculated using the Gasteiger-Marsili method and the semi-empirical MOPAC method [17].

Partial Least Squares analysis (PLS)

The PLS analyses were done by following standard protocols [18]. In order to speed up the analysis and reduce the amount of noise, column filter was used by excluding the columns with a variance smaller than 2.0. Equal weights for the steric and electrostatic descriptors were assigned using the CoMFA scaling option.

CoMFA Results

Two CoMFA models were generated by using different types of partial atomic charges, results of which are shown in Table 2. Model A was derived using charges calculated according to Gasteiger-Marsili method, while Model B was obtained using MOPAC charges. From the results it can be observed that both the models are significant in term of their statistical acceptance, however model B was considered to be better due to higher correlation coefficient and Fischer’s statistical value.

  Model A Model B
R2cv 0.561 0.598
S E P 0.381 0.377
r2 conventional 0.886 0.964
S.E. 0.194 0.112
Nopt 4 6
F value 58.344 126.195
P value 0.000 0.000
Steric contribution 0.418 0.428
Electrostatic contribution 0.582 0.572
r2BS 0.925±0.019 0.986±0.005
SDBS 0.051±0.017 0.046±0.007

Table 2: Summary of comfa results

Prediction of Activity

The 3-D QSAR analysis obtained as Model B was used for predicting the activity of the 33 compounds in the training set. The results are shown in Table 3. From the table, it can be seen that the predicted activities are very close to the experimental activities with minimum residual activity.

Compd. pMIC experimental pMIC predicted Residual
No.     activity*
1 0.74 0.72 0.02
2 0.84 0.77 0.07
3 0.64 0.65 0.07
4 0.37 0.38 -0.01
5 0.78 0.81 -0.03
6 0.34 0.32 0.02
7 0.88 1.03 0.15
8 1.29 1.22 0.06
9 0.86 0.90 -0.04
10 0.99 0.82 0.16
13 1.88 1.87 -0.01
14 1.46 1.59 -0.13
15 1.41 1.55 -0.13
16 1.47 1.38 0.08
17 1.35 1.32 0.03
18 1.45 1.25 0.19
19 0.79 0.87 -0.07
20 0.91 1.07 -0.16
21 2.00 1.97 0.03
22 1.44 1.37 0.07
23 1.64 1.70 -0.06
24 1.77 1.69 0.09
25 1.69 1.67 0.01
26 1.68 1.78 -0.10
27 1.25 1.28 -0.03
28 1.76 1.77 -0.01
29 1.78 1.77 0.01
30 1.70 1.68 0.02
31 1.65 1.69 -0.04
32 1.74 1.72 0.02
37 1.09 1.13 -0.04
38 1.29 1.19 0.01
39 0.53 0.64 -0.11

Table 3: Predicted and experimental activities of training set

CoMFA contour maps

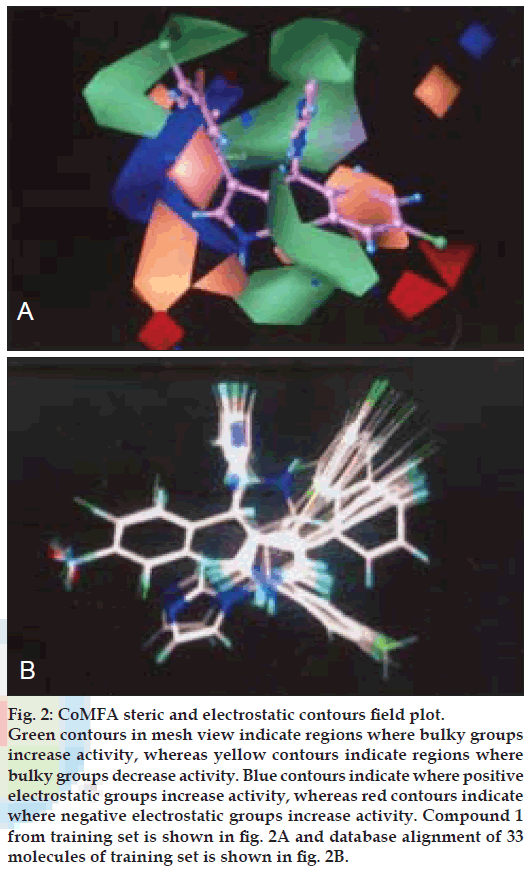
The QSAR produced by CoMFA were represented as a 3-D coefficient contour map. To visualize the CoMFA steric and electrostatic fields from PLS analysis, contour maps of the product of the standard deviation associated with CoMFA column and coefficient (SD Coeff) at each lattice point were generated. The contour maps were plotted as percentage contribution to the QSAR equation and were associated with difference in biological activity.

The CoMFA contour maps generated for model B were used to explain the structure activity relationship of antifungal drugs.

In CoMFA contour maps, the regions of high and low steric tolerance are shown in green and yellow polyhedra, respectively. CoMFA electrostatic field are shown as blue and red polyhedra in fig. 2. A low electron density within the inhibitors near blue and red polyhedra, respectively increase or decrease the activity.

Figure

Figure 2: CoMFA steric and electrostatic contours field plot. Green contours in mesh view indicate regions where bulky groups increase activity, whereas yellow contours indicate regions where bulky groups decrease activity. Blue contours indicate where positive electrostatic groups increase activity, whereas red contours indicate where negative electrostatic groups increase activity. Compound 1 from training set is shown in fig. 2A and database alignment of 33 molecules of training set is shown in fig. 2B.

Results and Discussion

The validity of Model B was further enhanced by bootstrapping process. Bootstrapping of 10 runs gave r2 of 0.986±0.005 with a very low standard error of 0.046±0.007 which added to the high confidence limit to this analysis. It can be seen that, both steric and electrostatic fi elds contributed to the QSAR equation by 42.8 and 57.2%, respectively. This suggested that variation in the antifungal activity is predominantly determined by electrostatic properties. Thus the results suggested that there is a good internal consistency in the data set generated in model B.

Model B performed exceptionally well in predicting the activity of most compound used in the test set. However, it must be emphasized that molecular alignment and conformations used in this study were selected in the absence of X-ray crystallographic coordinates of these molecules; still, the CoMFA model generated in the study showed very good prediction capability. From the Table 4, it can be observed that the predictions made using CoMFA model were satisfactory in most cases. In general, the percentage difference in the predicted activity of the synthesized compound ranges from 1.2 to 28.5%. The relative difference in the prediction is not unexpected and is within the acceptable limits.

Compd. pMIC pMIC Residual % Residual
No. experimental predicted activity  
11 0.87 0.89 -0.02 2.2
12 0.53 0.63 -0.10 15.8
33 1.68 1.69 -0.01 1.5
34 1.86 1.76 0.10 5.6
35 1.67 1.65 0.02 1.2
36 0.98 1.20 -0.22 18.3
40 1.10 1.54 -0.44 28.5

Table 4: Comparative variation in the experimental and predicted anticandida activity of compounds in test set

From these results, it is inferred that the 3-D QSAR model generated in this study has a potential to predict the activity of diverse compounds belonging to similar structural class. The investigations concerning the design of new chemical entities based on the proposed CoMFA models, predicting their antifungal activity prior to the synthesis would be part of our forthcoming communication.

Acknowledgements

The authors wish to thank His Holiness Jagadguru Sri Sri Shivarathri Deshikendra Mahaswamigalavaru of Suttur Mutt, Mysore, for providing the facilities to carry out the research work and All India Council of Technical Education (AICTE), New Delhi for financial support through MODROBS scheme.

References